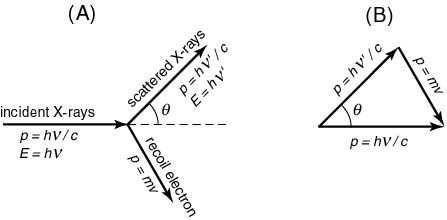
Compton Effect Crack PC/Windows Compton scattering is a scattering process, which means that a photon is scattered off of an electron. In a classical collision the initial momentum of the photon is conserved in the collision, while the initial energy is decreased. The probability that a photon will be scattered increases as the electron becomes more energetic, and the most probable angle of scattering is the angle between the incident photon and the electron. Scattering Angle: The scattering angle is the angle between the initial direction of the incident photon and the final direction of the scattered photon. Mentor: Dr. Christopher Gore, Bibliography Compton, A. H. The Compton Effect. External links K.W. Clayton (2009) "Compton Effect" Category:Photochemistry Category:PhotonicsQ: Passing in a generated View to MVC3 I am trying to dynamically generate an html page based off of a model that I am passing in. It seems that when I generate the html page as a string, I am not able to pass in the variables that I am requesting from my controller. I am trying to generate a drop down that will be populated based on the records in my model. The model has two parts, the first is the id for the items that I need and the second is the description. Here is my code: var client = new WebClient(); var htmlstring = client.DownloadString(""); var fahrzeug = htmlstring.Split('')[0].Split('')[1].Split('')[0]; var result = $""; foreach (var item in Model.Fahrzeuge) { result += "" + item.Name + ""; } result += ""; ViewData["ViewDropDown"] = result; However, when I try to retrieve the ViewData item, I get a null value for the Compton Effect Crack+ With Key Download (Final 2022) This macro simulates the scattering of light off of an electron. It is based on the relationship between light and energy. The macro takes 3 inputs: - The wavelength of the light (String) - The kinetic energy of the electron (Double) - The angle between the incoming light and the incoming electron (Double) Using this information, the macro then performs the following calculations: - Calculates the energy of the photon - Calculates the energy of the electron - Calculates the new energy of the electron - Calculates the photon energy as a fraction of the electron energy - Calculates the wavelength of the light - Calculates the new wavelength of the light - Calculates the final energy of the electron - Calculates the change in angle between the incoming light and electron Once the macro has finished its calculations, it prints to the clipboard the following: - New wavelength of the light (String) - Old wavelength of the light (String) - Difference in wavelength (String) - New wavelength of the electron (String) - Old wavelength of the electron (String) - Difference in wavelength (String) - New kinetic energy of the electron (Double) - Old kinetic energy of the electron (Double) - Difference in kinetic energy (Double) - New angle between the electron and the light (Double) - Old angle between the electron and the light (Double) - Difference in angle (Double) The simulation is based on the work of Compton (1923) and the momentum and energy equations derived in the process. The model was also tested against equations derived from the complete treatment of light-electron scattering (Compton, 1923). This macro was developed for the AVS Physics Workbench on a Windows 7 operating system. SUMMARY: This macro simulates the scattering of light off of an electron. It is based on the relationship between light and energy. The macro takes 3 inputs: - The wavelength of the light (String) - The kinetic energy of the electron (Double) - The angle between the incoming light and the incoming electron (Double) Using this information, the macro then performs the following calculations: - Calculates the energy of the photon - Calculates the energy of the electron - Calculates the new energy of the electron - Calculates the photon energy as a fraction of the electron energy - Calculates the wavelength of the light - Calcul 1d6a3396d6 Compton Effect X64 The effect of the electrons is to scatter light, when an electron is struck by a light photon it may be set free (relaxed) or knock the photon out of the way. The electron may not be set free from the photon, in which case it will recoil. If an electron in an atom is struck by a light photon, it may be knocked free from the atom, leaving the electron in an excited state. This can continue until the electron returns to its original energy state, the electron-photon bound state. The electron and photon are set free into the bound state. The scattering of the photon from an atom changes the energy of the photon. The binding energy of the electron-photon bound state is less than the free electron-photon bound state. The process involves the loss of an energy, and the atom releases energy of the photon and electron. The Compton effect may be described by the following equations, see for example Quantum Theory of Scattering of Electromagnetic Radiation, by G.H. Derbenev, Academic Press, New York, 1969, Eq. 1.8-1.9. (a) Energy loss of the electron due to the scattering 2E1+E0xe2x88x92kSxe2x80x83xe2x80x83Eq.(1.8-1a) (b) Energy loss of the photon by electron E0xe2x88x92kSxe2x80x83xe2x80x83Eq.(1.8-1b) (c) Energy change of the bound electron-photon state E2=E1+E0xe2x88x92kSxe2x80x83xe2x80x83Eq.(1.8-1c) where E0 is the binding energy of the electron-photon bound state, and E1 is the binding energy of the free electron-photon bound state. E2 is the binding energy of the electron-photon bound state after the scattering. The most significant aspects of the Compton effect are that light may be scattered in a manner similar to a particle. Electromagnetic radiation with its two components, a wave and a particle, is like a wave and a particle. It may be scattered by electrons or atoms in a manner that depends on the momentum of the photon and the energy of the electron. The result is a change in the wavelength What's New In? Explanation of the Compton Effect: Compton Theory: Explanation of the Compton Theory: Interpretation of the Compton Theory: What is the biggest problem in Compton Theory?: The biggest problem with the Compton effect is that it is largely dependent on the number of electrons in the atom. For example, if one atom contains eight electrons, then the ratio of light scattered off of the tightly held electrons is only 1.1 percent. If one atom contains 28 electrons, the ratio increases to 7.1 percent. If an atom contains 92 electrons, then the ratio increases to 32.2 percent. In practice, most atoms have few electrons and the Compton effect is small, but it is interesting to note that the Compton effect is not the same for every atom. When examining light scattering, one would think that if two atoms of the same type are examined, they should have the same scattering patterns. However, this is not the case. The ratio of electrons to protons in an atom does not guarantee the scattering patterns. The scattering patterns are affected by the charge distribution of the atom. This is caused by the potential energy between the electrons and protons in an atom. In some atoms, there are more electron-protons attractions than in other atoms. This causes the electrons to be more tightly held together and have less room to move in an atom. The electrons are less likely to scatter light. One could hypothesize that the two-electron scattering pattern is double the proton scattering pattern. This would make sense if the electrons were uniformly distributed around the nucleus, but that is not the case. The electrons are not evenly distributed around the nucleus. They are mostly concentrated in a thin layer around the nucleus with a small halo. An electron could be considered a sphere with a radius of 0.5 fermi. It would have a potential energy of 4 electronvolts. The nucleus would have a potential energy of approximately 24 electronvolts. The ratio of the potential energy between the two would be about 0.25 (4/24). When the nucleus is a proton, the potential energy between the electrons and protons would be approximately 4.5 eV. The ratio of potential energy between the two would be about 0.6 (4.5/24). Compton Theory Evaluation: Compton Theory works because it depends on the ratio of potential energy between the electrons and the protons. With the same ratio of potential energy between the electrons and protons, the Compton effect would not be different in the two atoms. It has been found that the Compton Effect does not depend on the number of electrons in an atom. The Compton Effect does depend on the ratio of the potential energy between the electrons and the protons. Compton Effect: Photon-electron Scattering: Compton System Requirements For Compton Effect: Windows XP, Vista, or Windows 7 1 GHz CPU 1GB RAM 2GB hard disk space How to Play: Aim and shoot the enemy zombies with the E-Shotgun and avoid the bullets of the zombies and the zombie-shooting gun of your enemies! Earn points to unlock new levels. The game can also be played as a highscore game. When you win a match, you can collect points and level up your player. The player with the most points after 15 matches wins the match.
Related links:
Comments